Algebraic Calculations

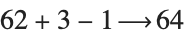
One of the important features of the Wolfram System is that it can do symbolic, as well as numerical calculations. This means that it can handle algebraic formulas as well as numbers.

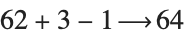
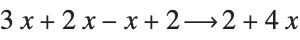
The Wolfram System automatically carries out basic algebraic simplifications. Here it combines 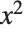and 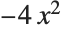to get :

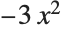You can type in any algebraic expression, using the operators listed in "Arithmetic". You can use spaces to denote multiplication. Be careful not to forget the space in xy . If you type in xy with no space, the Wolfram Language will interpret this as a single symbol, with the name xy , not as a product of the two symbols x and y .

When you type in more complicated expressions, it is important that you put parentheses in the right places. Thus, for example, you have to give the expression 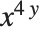in the form x^ ( 4y ) . If you leave out the parentheses, you get 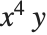instead. It never hurts to put in too many parentheses, but to find out exactly when you need to use parentheses, look at "Operator Input Forms".

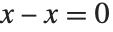
When you type in an expression, the Wolfram System automatically applies its large repertoire of rules for transforming expressions. These rules include the standard rules of algebra, such as , together with much more sophisticated rules involving higher mathematical functions.

The Wolfram System uses standard rules of algebra to replace 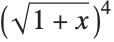by :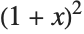

The Wolfram System knows no rules for this expression, so it leaves the expression in the original form you gave:

The notion of transformation rules is a very general one. In fact, you can think of the whole of the Wolfram System as simply a system for applying a collection of transformation rules to many different kinds of expressions.

The general principle that the Wolfram System follows is simple to state. It takes any expression you input, and gets results by applying a succession of transformation rules, stopping when it knows no more transformation rules that can be applied.

There are often many different ways to write the same algebraic expression. As one example, the expression 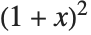can be written as 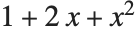. The Wolfram System provides a large collection of functions for converting between different forms of algebraic expressions.

There are many situations where you want to write a particular algebraic expression in the simplest possible form. Although it is difficult to know exactly what one means in all cases by the "simplest form", a worthwhile practical procedure is to look at many different forms of an expression, and pick out the one that involves the smallest number of parts.

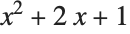
Simplify writes in factored form:

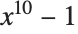
Simplify leaves in expanded form, since for this expression, the factored form is larger:

You can often use Simplify to "clean up" complicated expressions that you get as the results of computations.

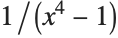
Here is the integral of . Integrals are discussed in more detail in "Integration":

Differentiating the result from Integrate should give back your original expression. In this case, as is common, you get a more complicated version of the expression:

Simplify is set up to try various standard algebraic transformations on the expressions you give. Sometimes, however, it can take more sophisticated transformations to make progress in finding the simplest form of an expression.

FullSimplify tries a much wider range of transformations, involving not only algebraic functions, but also many other kinds of functions.

For fairly small expressions, FullSimplify will often succeed in making some remarkable simplifications. But for larger expressions, it can become unmanageably slow.

The reason for this is that to do its job, FullSimplify effectively has to try combining every part of an expression with every other, and for large expressions the number of cases that it has to consider can be astronomically large.

Simplify also has a difficult task to do, but it is set up to avoid some of the most time ‐ consuming transformations that are tried by FullSimplify . For simple algebraic calculations, therefore, you may often find it convenient to apply Simplify quite routinely to your results.

In more complicated calculations, however, even Simplify , let alone FullSimplify , may end up needing to try a very large number of different forms, and therefore taking a long time. In such cases, you typically need to do more controlled simplification, and use your knowledge of the form you want to get to guide the process.

Some transformations used by Simplify and FullSimplify , for instance reduction with respect to equational assumptions, need to pick an order of variables. Therefore, results of simplification may depend on the names of symbols.

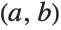
Reduction with respect to the equational assumption using the variable order leads to a simplification:

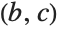
With the variable order , the expression is not simplified:

Complicated algebraic expressions can usually be written in many different ways. The Wolfram Language provides a variety of functions for converting expressions from one form to another.

In many applications, the most common of these functions are Expand , Factor , and Simplify . However, particularly when you have rational expressions that contain quotients, you may need to use other functions.